Creating A Pythagorean Oval

Mathematically, or even scientifically, I’m not sure whether there is such thing as a Pythagorean Oval, but in the images below you’ll see how a supposed Pythagorean Oval can be created using the calculations of Pythagoras’ Theorem.

Step 1

Step 1 is easy. Simply create your 3 by 4 rectangle.

Step 2

Now, divide your 3 by 4 square to create your Pythagorean 3, 4, 5 Triangle.

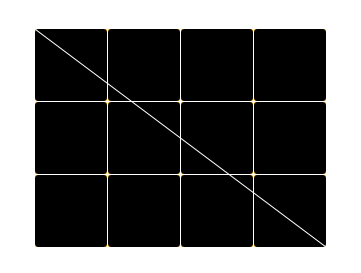
Step 3

Now we display the theorem which states that a² + b² = c² based on a right angle triangle.

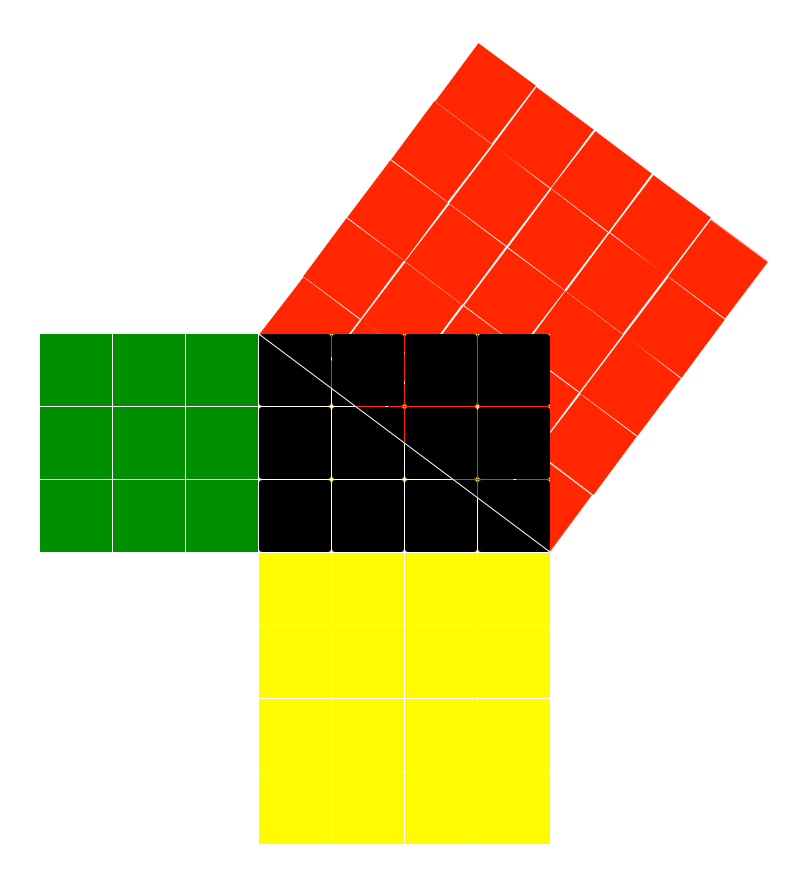
So we’ve all seen this before; probably in high school, maybe later; maybe while studying Sacred Geometry or you’ve heard of it through Masonry. Either way, the equation is, the hypotenuse squared will be equal to the length of the other 2 sides squared. in our case above, it will be 4² + 3² = 5² or 25. That’s that, but that’s not why we’re here. We’re here to create a Pythagorean Oval.

Step 4

As some in the Esoteric Kingdom say, “As it is above, so it is below” and so let’s add the square roots to the other right angle, the other half of the black rectangle, the one above it. (see step 1 for an idea of both sides of the rectangle, when divided into right triangles)

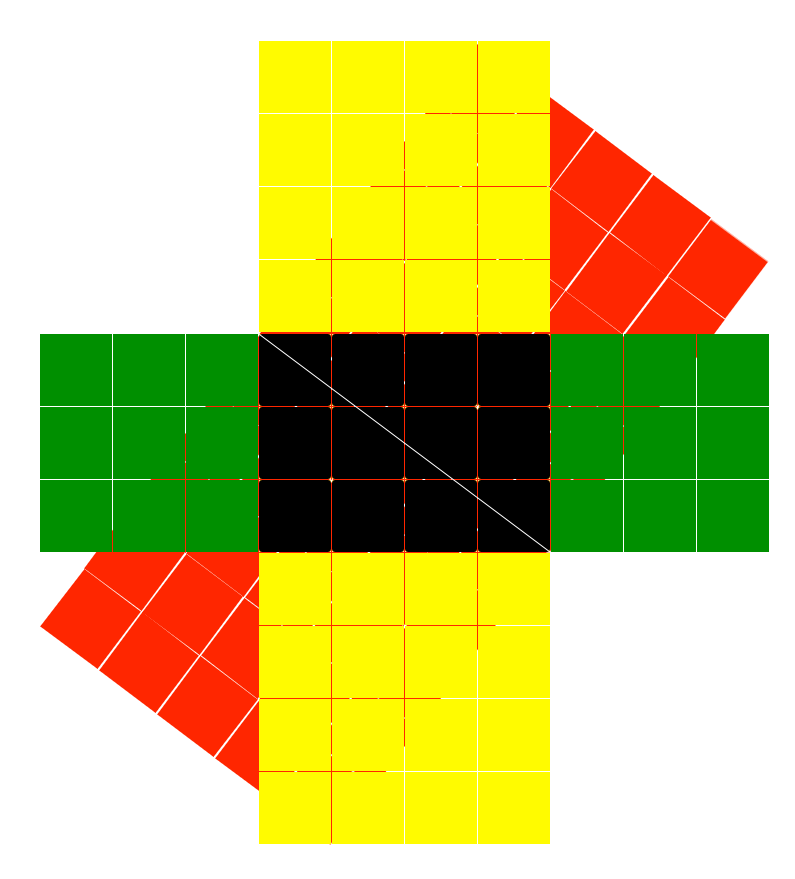
Now we not only see an interesting cross, but the genius Alchemist, and 1 who practices Sacred Geometry can surely find many more symbolic correlations besides a cross, but we’ll leave those observations for the ones who want to leave their comments below.

Step 5

Now, simply create your oval by ensuring the edges of your oval reach to the far reaches of the combined shape above, which is a Pythagorean Triplet from above and from below, as follows:

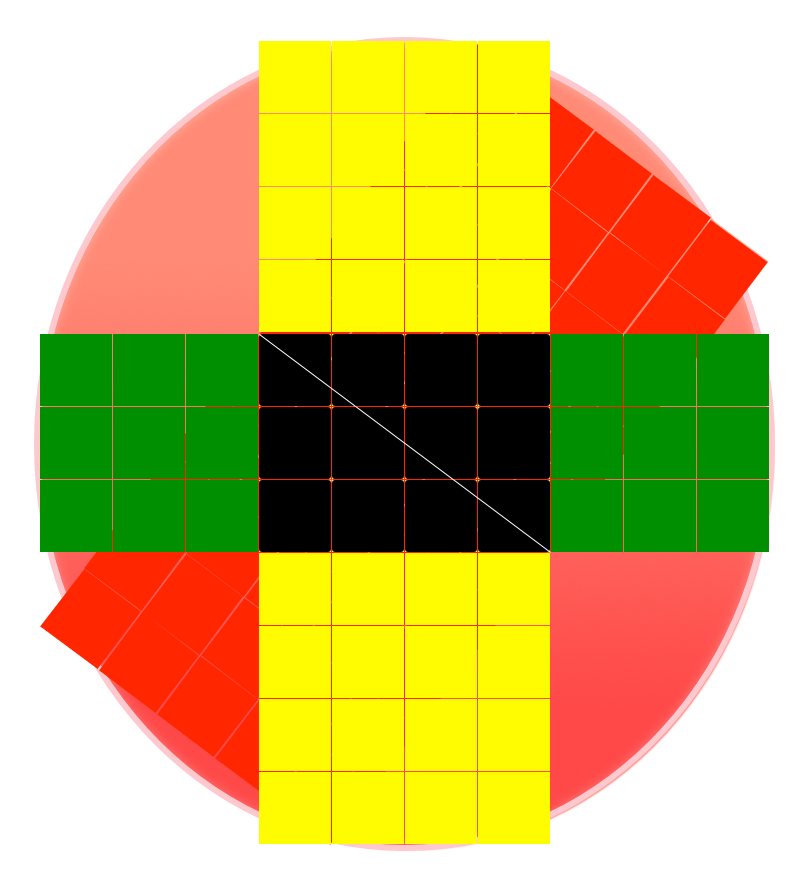
Step 6

You can see it’s not a “perfect circle” and it’s definitely an oval, and clearly created through the Pythagorean Theorem which was conveyed above and below the initial black rectangle. If we remove the divided black rectangle and it’s triplets from above and below, we are left with a geometrically sound Pythagorean Oval below.

I added a clipping mask just for fun. I hope you found this interesting and as I mentioned earlier, feel free to leave comments, observations or criticisms below. All are welcome.